Introduction to Statistical Inference

현재 정리하는 내용은 KAIST EE의 이융 교수님, Probability and Intorductory Random Process 강의를 참고하여 작성했습니다.

What is Statistical Inference?

• 몇 개의 예제를 통해 Inference가 무엇을 의미하는지 확인해보자.
  1. Take 1000 voters uniformly at random, and count the popularity of each candidate to infer the true popularity.
     → What is true popularity?
  2. COVID-19 has spread over a collection of people, and we collect a sample of COVID-19 infectees to infer the true source of infection.
     → What is true source of infection?
  3. When an original signal S is transmitted over the School Wi-Fi connection, the received signal X becomes X = aS+W, where 0 < a < 1 and W ~ N(0, 1). If we have 10 samples of (S, X) values, what is the inferred value of a?
     → What is value of a?
• 위 3가지 예제를 통해 Inference는 정보를 추출해내는 Process라는 것을 알 수 있고, 이 때 unknown variable or an unknown model을 기반으로 한다는 것을 알 수 있다.
  

Statistical Inference : Three Main Ideas.

• 앞서 말한 내용에서 주된 3가지의 아이디어를 생각해보자.
  1. Samples are likely to be a good representation of the unknown.
  2. There exists uncertainty (i.e, noise) as to how well the sample represents the unknown.
  3. How to obtain samples has impact on inference

Inference, Real World, Probability Theory

• 이 세 가지의 연관성을 알아보자.
  
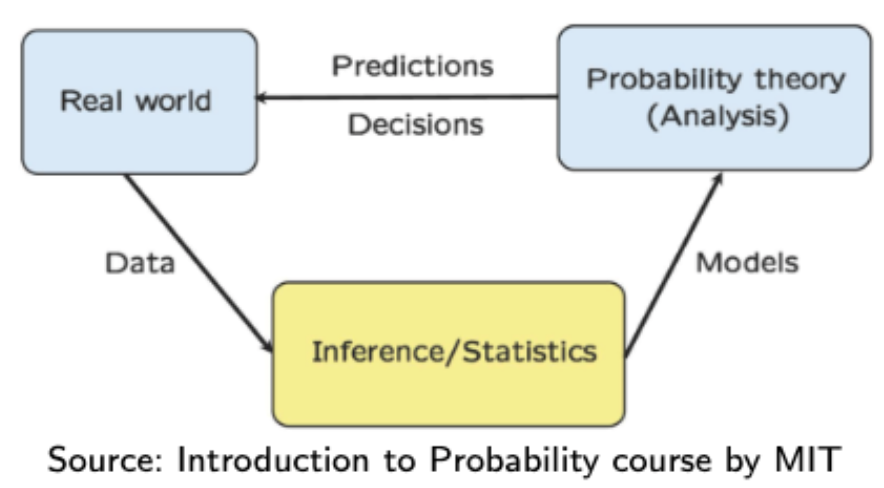
  → 그림에서 나온 것과 같이 세 가지는 모두 연관이 되어있다.
• Inference
  → 현실 세계의 데이터를 갖고, probabilistic model 또는 parameters를 결정하는 것
  

What to infer? Unknown Model vs. Unknown Variable

• 이 둘의 차이가 무엇일까? 앞서 예제에서 봤던 것 중 하나를 가져와보자.
  → When an original signal S is transmitted over the School Wi-Fi connection, the received signal X becomes X = aS+W, where 0 < a < 1 and W ~ N(0, 1). If we have 10 samples of (S, X) values, what is the inferred value of a?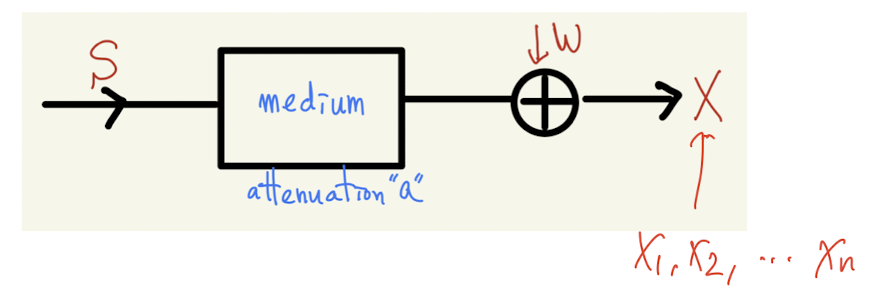
  
  → X = aS + W
  

  Model Building	Variable Estimation
  Know the original signal S Observe X Infer the model parameter a	Know the original signal S Observe X Infer the original signal S

• 이 둘의 다른 점은 있지만, 즉 다른 질문을 던지지만 동일한 수학적 구조를 갖게 된다.

  
  

What kind of inference? Hypothesis Testing vs. Estimation

Hypothesis Testing	Estimation
Unknown : a few possible ones. → Finite discrete Goal : small probability of incorrect decision → How can we evaluate my decision? Ex. Something detected on the radar. Is it a bird or something?	Unknown : a value included an infinite, typically continuous Goal : Finding the value close to the true value. Ex. Biased coin with unknown prob. of head. What is data of heads Note. If u have the candidate values of {1/4, 1/2, 3/4}, then it’s a hypothesis testing problem.

Different views: Bayesian vs. Classical

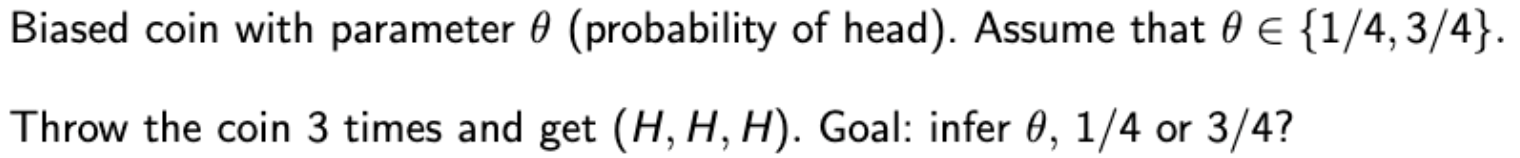
→ Infere할 것이 {1/4, 3/4}이므로, Hypothesis testing.
→ 직관적으로 생각해본다면, HHH가 나왔으니까 3/4일 확률이 더 높다. 이걸 Bayesian 관점과 classical 관점으로 확인해보자.

Bayesian View	Classical View
→ Prior distribution을 통해 posterior를 계산하는 전형적인 Bayesian 방법이다. → 가장 큰 θ를 고르는 방식은 MAP라고 한다. 후에 나온다.	→ 옆에 있는 Bayesian과 다르다는게 느껴진다. → θ가 있다는 가정 하에 HHH일 확률을 구하는 방식으로 한다.

• 이거는 Bayesian rule 계산 방식
  
  

• 수식으로 확인해보았으니 이제 글로 확인해보자.
  

  Bayesian View	Classical View
  Unknown : RV with some distribution (prior) Observe : Data X, posterior distribution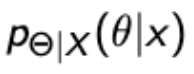 → 표본으로부터 제공된 정보와 함께 unknown parameter의 확률 분포에 대한 지식을 사용하여 추론	Unknown : Deterministic value Observe : Data X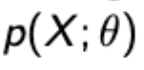

• 그럼 누가 더 좋은 방식이야?
  → 이것에 대한 정답은 아직 없다. 아래 예제를 한 번 확인해보자.
• Example. mass of the electron by noisy measurement.
  Classical View : unknown이기는 한데,,,전자의 질량은 당연히 상수지. 그러니까 모델링할 수 있는 RV는 없어.
  Bayesian : 아니! 우리는 some range of candidate values를 이전 측정에서 구할 수 있으니까 당연히 가능해!
• 이렇게 서로 다른 주장을 할 수 있다. 따라서 누가 더 좋고 말고 할 것이 없다.
• 근데, Bayesian은 다차원 데이터에 대한 계산의 용이성이 있다는 점은 존재한다.
  → MNIST는 28 by 28의 다차원 데이터이다.